Recovering blackbox block cipher configuration and a rant
They're basically just really big substitution ciphers, right?
Home Tools List Guides Puzzles BlogsIntroduction
*I'll prefix all this by saying that I'm some random bloke on the internet, don't take anything I say as gospel in regard to cryptographic security/practices*
Table of contents:
If you've spent much time around any community using cryptography, you'll eventually come across seemingly random looking text such as:
oo9PlvAB2YDcwqV+qDaneauK1Sy6ewmWkduPSqDwKE0/OxMBkzTECC3bLrdBt4RY
Depending on how much experience you have you'll approach this in a few different ways. If you know the basic tropes you'll likely confidently say "That's base64" (You wouldn't be wrong mind you), but be left confused after decoding it and being met with random looking data. A step up and knowing that base64 is just an encoding for safely transporting raw data (Which could be anything itself) you might try analysing the underlying data. Maybe it's transporting a binary format file, maybe a simple XOR encryption, but quickly hit a dead end.
It's more than likely you're dealing with some kind of modern encryption (We'll touch on alternatives later), likely a specific website's implementation of one. These aren't inherently bad, and do have their use-cases, but they're often used in an obnoxious fashion. Online sites in particular are the worst offender which we'll be focusing on here as opposed to something like local OpenSSL.
The crux of the issue really comes down to the fact that you can't just say "This is AES, the password is 'hello'".
- AES what? 128/192/256?
- Chaining mode? ECB/CBC/CTR...
- What KDF was used, what parameters?
- What IV?
- And so on...
The issue only compounds when the password or algorithm isn't known with certainty.
With local encryption (Anything you have control over in general) you at least have the chance to give or hint at these settings. But with sites you don't even know these yourself and have to explicitly give the site itself instead. It's an exception rather than the rule for different modern encryption sites to be compatible with each other, so without knowledge of the site it just turns into a guessing game. This effectively results in a proprietary encryption exclusive to whatever site was used, and more often than not you're not even given the site.
This combined with privacy concerns (The server will recieve your plaintext) and digital data-rot (What happens to your ciphertexts if the website goes offline or their setup is changed? This has already happened to the two most popular sites in the past) mean it would be nice to recover whatever settings they're using to avoid being reliant on them, for quickly checking ciphertexts across multiple sites in a concise manor, or to open up other analysis that would only be possible locally.
Identification
We'll start off by actually identifying how likely some unknown string is to be encrypted in this way, and then move on to specific sites.
When used properly modern ciphers have very good randomness characteristics, generally indistinguishable from noise. So it might surprise you that there's actually quite a lot of literature on distinguishing specific modern ciphers between each other [10.7717/peerj-cs.1110] with accuracy better than pure chance.
We'll however be using much more primitive indicators, namely the entropy and length while also building off of context and what's commonplace / established.
In this context entropy is a measure of how disordered a system is. If we look at a binary sequence of length 128 (1 AES block) there are a lot more unique states it could be in that have high disorder compared to ordered. So we'd expect random data to prefer the more numerous states and have high disorder and thus high entropy.
Very ordered ascii, leading bit is always 0 with patterns elsewhere:
01001000 01100101 01101100 01101100 01101111 00100000 01010111 01101111 01110010 01101100 01100100 00100001 00100000 01100110 01101111 01101111
Compared to random data, no patterns:
10010011 00010101 11011100 01001100 00111001 10000001 00011010 10011011 11100111 10111001 10101001 11011111 10001000 01011001 10110111 10111101
Since modern ciphers should produce ciphertext indistinguishable from random data we expect such ciphertext to also have high entropy. Now from here we could use fancy statistics, normalised entropy from 0-1, but just looking at bog-standard Shannon entropy over a byte (256 symbols) will be plenty.
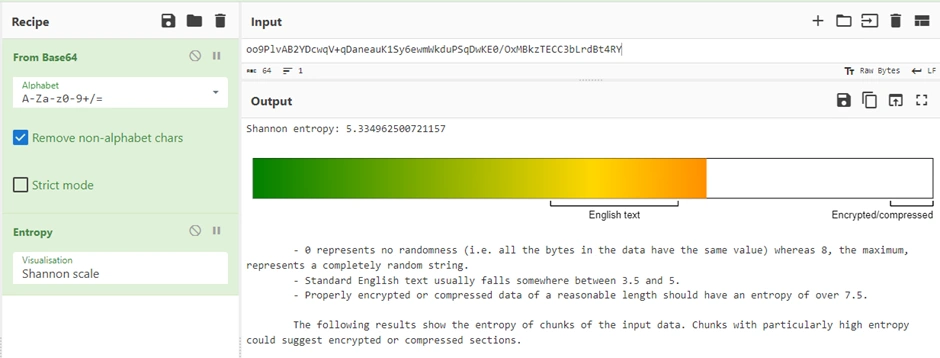
Let's look at the string from before in CyberChef. Note that this is non-normalised entropy so the "English text / Encrypted/compressed" markings are values that data tends towards as length increases and aren't representative for our small 48 bytes here. After all, you can get much more disorder from 1000 bytes vs just 10 bytes.
So instead, we'll use a quick and dirty method to check against encrypted (equivalent to random) data. We'll swap out our ciphertext input with the "Pseudo-Random Number Generator" operation set to give us 48 bytes of random data (Same length as our ciphertext holds). We then get an entropy of 5.41. This is higher than our ciphertext, but we're dealing with randomness and probability here, so checking a few more random generations and we see as low as 5.25 and as high as 5.54. Again, we could look at a histogram with Nth quartiles or get the standard deviation, but this is plenty for a rough indicator.
Given ASCII plaintext of the same length gives entropy of around 3.74 we can safely say our ciphertext has high entropy. But does that necessary mean it's encrypted with modern crypto? You might be tempted to wonder what if it's something obscure that just gives high entropy? Maybe it isn't base64 at all, a different base64 charset, or Vigenère on top of base64 carrying plaintext. But, for decently sized ciphertext, entropy is a fairly robust indicator, and it's pretty difficult to get such high entropy. Even interpreting a different b64 charset (carrying plaintext) with base64 low entropy will still shine through.
If there's any reason to suspect a different method to modern crypto for a ciphertext then generate a trial ciphertext of the same length using that method and check if its entropy is near the suspected ciphertext.
However, one real issue is compression. By its very nature it wants to reduce any ordered data into its smallest representative form, increasing entropy. Thankfully, a lot of compressed formats such as rar, 7z, jpg, png will have enough structure for an entropy lower than pure noise, and even better obvious magic bytes and file layout. But a zlib stream, or even worse a completely raw DEFLATE stream will have entropy comparable to encrypted data with little or no headers. Some common formats can be detected with Binwalk + Foremost while Offzip is very powerful for DEFLATE streams [http://aluigi.altervista.org/mytoolz.htm#offzip], but watch out for more obscure formats.
Finally, there's the length of the data. Modern symmetric encryption can be split up broadly into 2 categories:
- Block ciphers
- Stream ciphers
Block ciphers, unsurprisingly enough, work in blocks of fixed length. AES, the most common example, works in blocks of 16 bytes, but 8, 16, and 32 aren't unheard of for others. If you want to encrypt a plaintext that isn't a multiple of 16 it must be padded somehow up to that boundary. So if your ciphertext is a multiple of a common block size it's more likely to be a block cipher (Although not guaranteed as seen below). Rather confusingly, block ciphers can also be effectively used as a stream cipher in certain chaining modes such as CTR/OFB/GCM in which case they produce ciphertexts of any size.
Stream ciphers on the other hand produce ciphertext of any size but thankfully are less common in this context, so we won't be focusing on them here. But be aware there's nothing stopping a stream cipher from being a multiple of a block size and throwing you off, so length isn't the be all end all.
Recovery
Now we can at least tell with a decent degree of certainty if we're facing ciphertext from one of these sites. We could go through all the popular sites one by one every time we're faced with such a ciphertext, but that gets old quickly. So we'd like to be able to recover whatever parameters these sites use. This will also allow further local analysis that wouldn't be possible when limited to an online interface e.g. case stripped base64 AES.

The first and easiest parameter is the chaining mode. ECB and CBC are the most common. A pretty big flaw of ECB is that identical plaintext blocks will produce identical ciphertext blocks. This can be catastrophic for repetitive data such as images. You're less likely to get identical runs of 16 characters in text, so it can't commonly be used to distinguish ciphertexts in the wild. But there's nothing stopping us purposely giving a site a run of say, 80 a's, and looking at the result.
Such a result might look something like:
b6tvk7AGLgtzJJMSupeTuW+rb5OwBi4LcySTErqXk7lvq2+TsAYuC3MkkxK6l5O5b6tvk7AGLgtzJJMSupeTuW+rb5OwBi4LcySTErqXk7lD522VKEo0UR553BZouNnf
Or in hex:
6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 43 e7 6d 95 28 4a 34 51 1e 79 dc 16 68 b8 d9 df
And sure enough we see the 16 byte 6f ab 6f 93 b0 06 2e 0b 73 24 93 12 ba 97 93 b9 repeat itself meaning ECB was used. If we hadn't, we might suspect CBC.
If you're sure you're dealing with a block cipher but the resultant ciphertext increments in single bytes instead of block sizes, the mode may be something like CTR/GCM/OFB. GCM will probably tag on a few extra bytes (Usually 16) even to an empty plaintext's ciphertext for its authentication tag. It's also worthwhile being aware that a KDF salt or IV may be prefixed to a ciphertext as well.
We'll move onto plaintext padding now. It isn't the most vital parameter to know, but again it's good to at least be aware of. As all plaintext needs to be a multiple of whatever block size is being used (Bar stream-esque chaining modes) it needs to be padded somehow. PKCS7 or fixed byte padding are the two most commonly used. PKCS7 always reserves one byte, so if encrypting a plaintext of 1 block length results in 2 ciphertext blocks, that's an indicator for PKCS7 padding. For fixed byte padding it's a little trickier and could be left as the last parameter found by decrypting the ciphertext with the other known settings. If that isn't an option then encrypting a plaintext of 1 block length for a ciphertext 'A', then encrypting the same plaintext with the last byte replaced iterating through 0x00 to 0xFF untill the returned ciphertext matches A will recover the correct padding byte.
Now we've got an idea for the chaining mode and plaintext padding, what about the actual cipher? The distinguishers mentioned previously would be ideal, but as they're more academic and still with low accuracy, we'll have to make do with something else. Unfortunately, there really isn't much we can fall back to here bar any meta context around the site. However, if you can pin down the block size it can place some restrictions.
Now we'll move onto the key. Again, there isn't anything clever we can do here bar any meta information and trying the most common keys if the key is fixed or KDFs if a password field is offered such as:
- Padding with a specific byte (Usually 0x00)
- Concatenating password to itself N times + cropping to key size
- MD5/SHA256 + cropping to relevant key size
- PBKDF2 (May God have mercy in this case)
From a security viewpoint you'd want to use at least salted PBKDF2, or preferably something more modern and ASIC/GPU resistant such as scrypt or Argon2. But often these sites will go with one of the simpler methods. A nice catch all for the first 2 methods is to pass the site a key of whatever key size is relevant e.g. 16 bytes for AES 128. That'll remove some ambiguity because padding isn't being done and make finding out other parameters a bit easier.
Now we can move onto CBC with that troublesome IV. Firstly, it's important to note that with CBC an incorrect IV but correct key will still give a correct decrypt after the first block so only really becomes relevant with a single block ciphertext or if that first block is important.
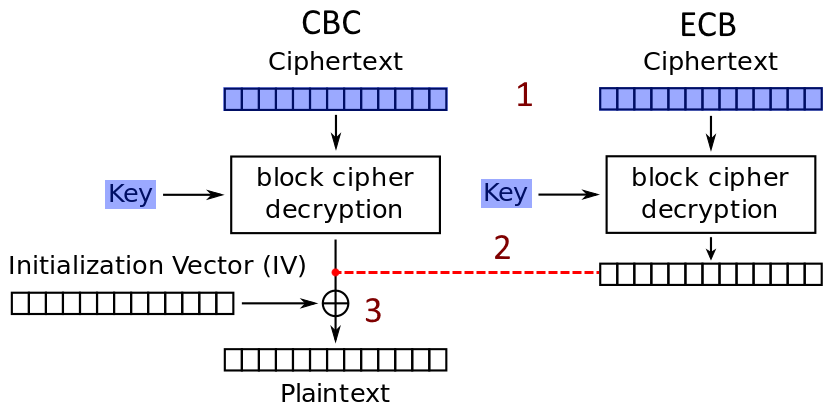
So while it isn't the end of the world if we don't have it, it would be preferred. Thankfully, there's a trick for recovering it. If we look at the CBC/ECB flowcharts during decryption for the first block we see CBC is basically just ECB with its output XORed against the IV. Meaning we can use ECB with the same key as a CBC encryption to decrypt the first ciphertext block, get the intermediate state of the CBC before XOR (2), and recover the IV as:
IV = Plaintext ⊕ CBC_I_STATE (2)
We could, of course, encrypt a null plaintext to skip this XOR step and get the IV directly, but some sites aren't big fans of letting you pass non printable bytes, and it isn't much trouble anyway.
We'll cover an explicit example in the case studies.
From here we may still have several options or unknowns for each parameter and it'll come down to bruteforcing. Generally though, the number of combinations is feasible.
Case Studies
Some of the explanations may have seemed pretty vague and unlikely to work out in practice. So to provide a more concrete example, and show that even with all the educated guessing it still often works out, here are a few case studies.
Partial - Online-Toolz
I know I'm only after saying these case studies are to prove everything works out, but I'll immediately go against that with one where only a partial recovery is possible to temper expectations. We won't be recovering any secure keys or cracking open AES here. Still, we'll see that even here, in the more difficult cases, we can extract a decent amount of configuration details.
The first thing to check is that the encryption is actually being done server-side or not, even obfuscated client-side would be preferred to server-side. Unfortunately, reading through the source shows that isn't the case here. A post request is sent with the plaintext, and a response containing the base64 ciphertext is returned.
So pretty much right off the bat we don't expect to fully recover everything on this one. There isn't a key/password option, limiting how much we can probe, and whatever default key is being used is kept server side.
Still, not to be dissuaded we'll start by checking the chaining mode and encrypting a single "a" which returns:
EsRtvLIlJ3O5HuNV1Bo824FOzjelsmHmtYFTcBk57/A=
32 bytes, kind of strange. Perhaps it's a 16 byte IV prefixed to a normal 16 byte block cipher? Let's see what happens with 17 "a"s:
lVPaeqMvNh2yO8TS+ExP6MQnJpFuY0jvmFS+gwe7hXc=
We didn't increment another 16 byte block as expected with a block cipher of that size, maybe we're dealing with a 32 byte block cipher?
Let's encrypt 32*4 "a"s:
RFwyvGxynwpq4/dvmBkhS9BwfgiuASbAGWPo+b5cCoFEXDK8bHKfCmrj92+YGSFL0HB+CK4BJsAZY+j5vlwKgURcMrxscp8KauP3b5gZIUvQcH4IrgEmwBlj6Pm+XAqBRFwyvGxynwpq4/dvmBkhS9BwfgiuASbAGWPo+b5cCoE=
And in hex:
44 5c 32 bc 6c 72 9f 0a 6a e3 f7 6f 98 19 21 4b d0 70 7e 08 ae 01 26 c0 19 63 e8 f9 be 5c 0a 81 44 5c 32 bc 6c 72 9f 0a 6a e3 f7 6f 98 19 21 4b d0 70 7e 08 ae 01 26 c0 19 63 e8 f9 be 5c 0a 81 44 5c 32 bc 6c 72 9f 0a 6a e3 f7 6f 98 19 21 4b d0 70 7e 08 ae 01 26 c0 19 63 e8 f9 be 5c 0a 81 44 5c 32 bc 6c 72 9f 0a 6a e3 f7 6f 98 19 21 4b d0 70 7e 08 ae 01 26 c0 19 63 e8 f9 be 5c 0a 81
And indeed we see repeated runs of the 32 bytes:
44 5c 32 bc 6c 72 9f 0a 6a e3 f7 6f 98 19 21 4b d0 70 7e 08 ae 01 26 c0 19 63 e8 f9 be 5c 0a 81
So we're pretty sure we're dealing with a 32 byte block cipher in ECB mode, but what one? Well there aren't many popular candidates. Funnily enough, the 3 that come to mind were all finalists for AES: Twofish, Serpent, and Rijndael. Out of these I'd hazard Rijndael to be the most popular, and as it's suspiciously present on the page we'll go with that for a working assumption.
As we're working with ECB there isn't much left that we can do. Can we at least figure out anything more with plaintext padding?
PKCS7 is probably the most common type of padding and always reserves at least a byte to itself. This means a 31 byte plaintext will encrypt to 1 block, but a 32 byte plaintext will encrypt to 2 blocks with the last block being entirely padding. Encrypting 32 a's:
RFwyvGxynwpq4/dvmBkhS9BwfgiuASbAGWPo+b5cCoE=
...gives just a single block, so we can rule out PKCS7. The next most likely is padding with a fixed byte, usually 0x00. Unfortunately, as we don't have control over the key we can't just decrypt a trial ciphertext to check. When decrypting a ciphertext the server handles all padding server-side and just sends the stripped plaintext back so that's out the window as well.
However, if we know encrypting 31 ‘a's give:
pfys7P2k3blPjtx4i5utzMFSUPBmtrFgzCktqYOjz8k=
Then there's only 1 byte of unknown padding being done. We can check all 255 bytes inserted into the 32nd position of the plaintext until we get the same ciphertext returned. I'm lazy so we'll just edit the request directly in Firefox (URL encoding the raw bytes) and check the most common padding values first as:

And we get lucky on the first try, adding a 0x00 byte gives us the same ciphertext as before. We can double check with 30 a's and adding 2 null bytes and it still works out.
So we know for sure:
- 32 byte block cipher in ECB mode
- 0x00 plaintext padding
And suspect the block cipher to be Rijndael.
We might try bruteforcing common keys using these setups but to no avail.
Unfortunately, that's about all we can gleam from this site, and we're left wondering if our assumptions are even correct. However, it just so happens the source was leaked recently (@corg0) meaning we can check what the backend was doing.
To sum it up, it was using mcrypt and Rijndael with a 32 byte block size and 16 byte key in ECB with null plaintext padding after all. Nice to have the confirmation. Also strangely enough generating and passing an IV which is of course unused in ECB. The key was 16 bytes of ascii, but definitely not within the realm of even a targeted bruteforce which explains our failure earlier.
Full - aesencryption.net
Now an example of a full recovery. Looking at the site we've now got access to a password and 3 different key-sizes (128/192/256) along with the site directly telling us it's using AES. It might be tempting to read into their example code provided as well, but we'll hold off on this for now and see how far we can get without it.
Again, it looks to be completely server-side, so we'll start by finding the chaining mode. Encrypting 16*4 a's gives us:
qLk0JXge1V2YcIYcnHPWc9rKfcqfXdnstojoS3tuiGSzBrSz4fzF3j1bS+8KksbWGaKcQy6EfFtQ4ZGIvoEgyWVs29tecUCgHkVfsGANKxs=
In hex:
a8 b9 34 25 78 1e d5 5d 98 70 86 1c 9c 73 d6 73 da ca 7d ca 9f 5d d9 ec b6 88 e8 4b 7b 6e 88 64 b3 06 b4 b3 e1 fc c5 de 3d 5b 4b ef 0a 92 c6 d6 19 a2 9c 43 2e 84 7c 5b 50 e1 91 88 be 81 20 c9 65 6c db db 5e 71 40 a0 1e 45 5f b0 60 0d 2b 1b
No matching blocks this time, so we're probably dealing with CBC meaning we'll have an IV to contend with. To recover it as laid out before we'll need to know the password. Thankfully we have control over it, but still need to figure out the KDF.
Let's hope for the simplest and try encrypting with 16 b's as the password, if it's a simple padding/duplicating KDF then this shouldn't be changed by them. We'll encrypt a few blocks so even with the unknown IV every block after the first will still decrypt correctly, allowing us to check if we've gotten the correct KDF. We'll just use a random IV at the moment, it shouldn't matter.
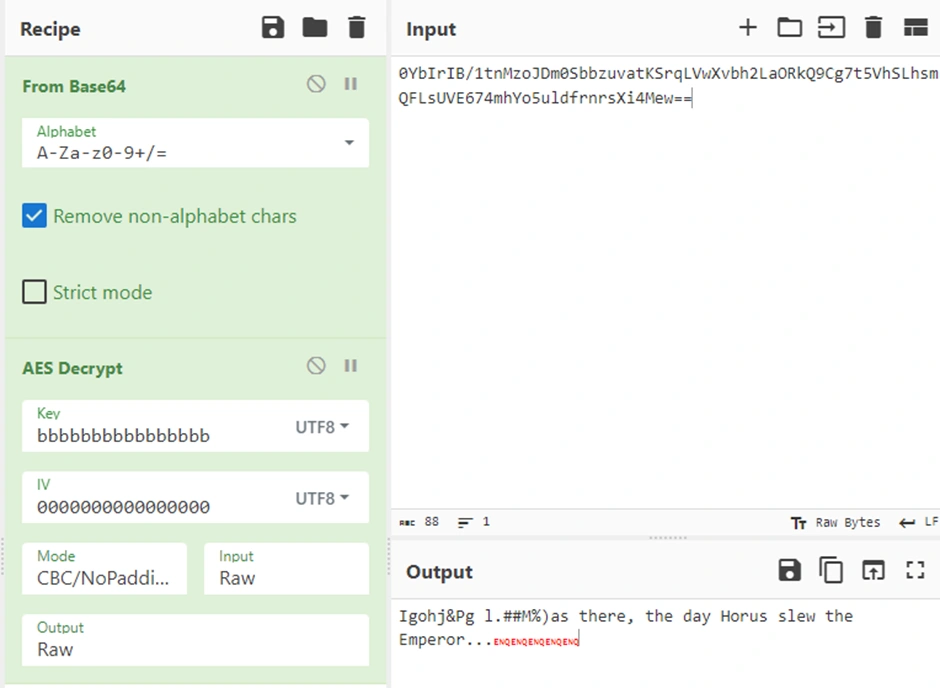
And we get lucky, it's either duplicating/padding the password for the key instead of doing anything fancy. We can even see PKCS7 padding being used here from the "0505050505" trailing bytes so it's a 2 for 1 deal.
Let's now encrypt the same payload with 15 b's leaving the last byte to the unknown padding for us to bruteforce.

We get lucky with 0x00, and after making sure it holds with different password lengths and key sizes we can say the "KDF" is just null padding to the desired key size.
Now all that's left is the IV. Following from the method outlined earlier we only care about the first block so we'll encrypt "Hello World!!!!" and leave the last byte to the PKCS7 padding along with the key of 16 b's meaning our plaintext is 48 65 6c 6c 6f 20 57 6f 72 6c 64 21 21 21 21 01 and our ciphertext is E0mE1rL+Wv3jkitL5cBT5Q==.
Decrypting this in ECB with the same key we get 79575f585a166057105c1e131215146f so the IV can be found as:
79575f585a166057105c1e131215146f ⊕ 48656c6c6f20576f726c642121212101
= 313233343536373862307a323334356e (12345678b0z2345n)
So it turns out the IV from the example code wasn't being used after all and would've sent us in the wrong direction.
The only thing left is to figure out the default key. Given the KDF is just null padding I wonder if that holds true even for no key, efficiently making it null? Encrypting a plaintext with no key and decrypting with the known IV and such a key and... we get lucky here and that indeed turns out to be the case.
And with that we've fully characterised the site as:
- AES CBC 128/192/256
- IV: 12345678b0z2345n
- Plaintext PKCS7 padding
- KDF null padding password to key size
- Null default password
Closing Comments
This has been a fairly general overview and you'll often have to take sites on a case-by-case basis. There may be more opportunities or restrictions, but the methods outlined here should be a good start.
What to do once we've actually gotten all this info? Well as previously mentioned making a database of the most common sites to check them all at once locally would be nice. Most of these sites also lack an intensive KDF, opening the door for wordlist/mask attacks. Thankfully Corgo has us covered here on both fronts with the previously mentioned https://corgi.rip/dive.
I also realise after criticising use of these sites I'm now on the hook to suggest alternatives. For serious encryption you definitely shouldn't be relying on most of these sites, and they should be viewed as light obfuscation at best. Secure alternatives include OpenSSL, GPG and VeraCrypt.
Even for puzzles you should consider something else. If not because of the chance of data rot then for the vulnerability of these sites to wordlists and the ambiguity they introduce for solvers. Alternatives include explicitly spelling out the settings used, CyberChef gives a fairly transparent AES interface and has a low ‘barrier to entry', but that can seem a bit strained. But there's nothing stopping you, and I've seen examples of each in the wild for puzzles/ARGs, from using the previously meantioned software. At the very minimum state whatever site was used if you must, there's nothing worse than having the correct password but not getting it because some obscure unexpected site/KDF was used.